Introduction
I jest, this will be somewhat long...
Limits - Find out what happens to a function as you approach a certain value.
Derivatives - Calculating rates of change.
Integration - Finding the area under a curve.
As noted previously, Integration and Derivatives are inverse operations, this is
called the "Fundamental Thereom of Calculus" or so I hope.
One can think of integration as finding the antiderivative if that helps at all.
Now as for limits you can manipulate them algebraically when you cannot get the
exact value that the limit approaches. Techniques such as difference of
squares, difference of cubes, or factoring in general to get around scenarios where f(whatever limit is) = DNE.
Derivatives have some nifty little rules that make your life easier when finding
rate of change, rules such as the power rule which essentially gives you the slope
of a tangent line of whatever original function. The tangent line is the line that
touches a curve at one point. A secant line touches a curve at two points.
To calculate the slope of a tangent function, you find the derivative of the function
at "x" point. To calculate the slop of a secant function, since you are given two points
which can be found via algebra: (y_2 - y_1)/(x_2- x_1). The slope of the secant line
gets closer to the slope of the tangent line as x gets close to whatever value;
limits thus are an important concept here to evaluate the slope of a tangent line.
The derivative is a function that gives us the slope of the tangent line at some
value.
You can estimate via the slopes of secant lines or use the limit method.
Example...
Using limit method to demonstrate, remember difference of cubes rule.
The derivative of any constant "C" would be zero (because it's a constant... try it out yourself).
Thus when crunching the anti-derivative, you'd inverse that too. Where derivatives are useful is that
you calculate rate of change, how fast something changes per unit of time. Integration helps you determine
how much something accumulates over a period of time (area under the curve).
versus
Just like how multiplication and divison are opposite processes if you squeeze your two remaining braincells together
you big old doofus.
Definite integrals are definite, there is a "limit" in that you have upper and lower bounds.
Indefinite integrals give you a function instead of a number.
Limits
As x goes to 2 from both directions, y=1 because x does not become 2 itself.
Graphically remember that: "-" minus = left, "+" = right.
"f" has a vertical asymptote at x=a means that at least one of
and
equals to
or
.
c: constant (fixed constant variable)
x: approaches “c”
secant touches 2 points
tangent touches 1 point
Where m is the slope of the tangent line derived from the secant.
represents change in x. TLDR;
We want as
approaches zero, for it to get arbitrarily close to 0, but never reach 0.
As this reaches zero the slope of the tangent can actually be found mathematically speaking.
The equal sign within the context of limits is an mathmematical equal sign.
At x = -1, this is undefined. substituting -1 in after factoring results in 2 for y which is what this
function nears as x gravitates to -1, but never reaches -1.
This one has to be factored as you cannot make a guess over an indeterminate which could result in a
number, DNE, or even infinity. Some more examples below…
Via substitution.
Via substitution.
Conjugates.
On the calculator check how the values behave the closer one reaches zero, yet not actually on zero.
Now with trig identities too with product of individual limits.
f(x) approaches L as x approaches c if the above is true.
If the above statement is true, then we say y=f(x) in continuous at x=c.
Integration
A situation where you need to figure out the rate of change would require differentiation such as
figuring out how fast is th eamount of water change in a tank at whatever specific time (thus making it instantaneous).
If a function is given in that situation representing the amount of water at any time, you'd just
find the derivative of that function and substitute in values at whichever time you need the
instantaneous rate of change for.
What if this is not the case? What if instead of finding the instantaneous rate of change, you want to
figure out how much water or whichever variable has accumulated from certain intervals? Well you'd want to
figure out the net change (definite integral) or the indefinite integral. Definite obviously having a lower and upper limit,
meanwhile indefinite gives you a function that you can substitute a variable in to figure out for example
how much water has accumulated by a certain time.
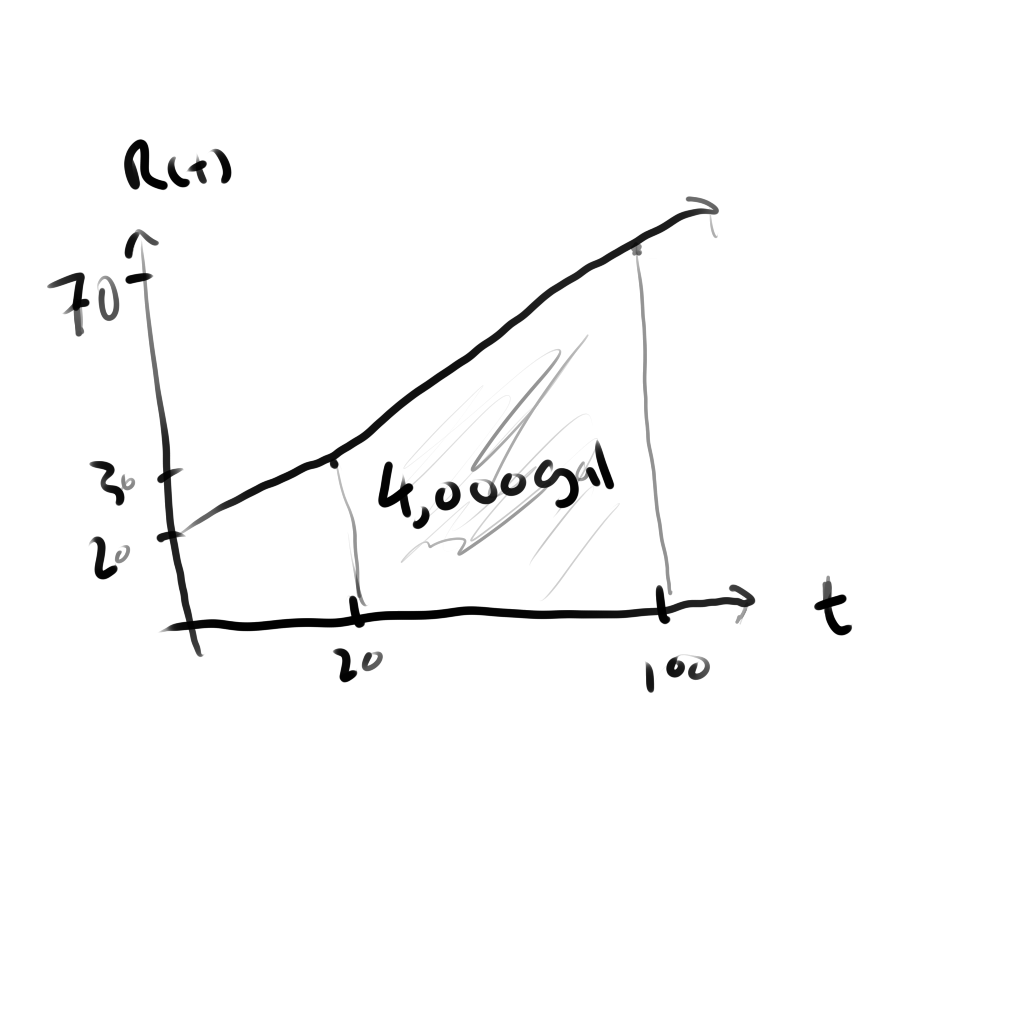
Question example: The rate of water flowing in a tank can be represented by the function R(t) = 0.5t + 20
where R(t) represents the number of gallons of water flowing per minute and t is the time in minutes. How
much water will accumulate in the tank from t = 20 to t = 100 min?
Without a lower and upper bound you'd just find the indefinite integral, however given such bounds you are seeking
the definite integral...
Differentiation
Slope of tangent (instantaneous change). If a function is differentiable at a point, then it must be continous there too.
Handy rules
1.
2.
3.
4.
5.
6.
Example(s)
Calculate ball velocity after it's in the air for one second.
Find the derivative (slope of the tangent line), then substitute in 1 which will find the slope at that
point which will tell you the velocity.
Find the derivative
Find
if
Implicit Differentiation
Not all derivatives fall into the neat little form where you can neatly represent in terms of
an independent variable. So you may have a function written in terms of both dependent and
independent variables.
The TLDR is that some functions do not define y (or whatever) as a function of x, thus you
can use implicit differentiation to find y with respect to x without solving for y.
Find dy/dx by implicit differentiation.
Examples
Combinatorics
Permutations
Permutations are suited for lists (order matters), a common example is that of
awarding prizes (1st, 2nd, 3rd). When you have a pool of 9 people for example, and can only award
three, the order that the medals are handed out matters. 1st place would have a pool of 9 people
to choose from, 2nd would have 8, 3rd would then have 7. A factorial is useful however
you only have 3 people out of 9...
9! = 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1
We can omit all but the first three corresponding with the 3 prizes.
9!/6! = (9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1)/(6 * 5 * 4 * 3 * 2 * 1) = 9 * 8 * 7
Or as one can describe in a formula where we have "n" items in total and "k" being the number of items
that can be ordered:
P(n,k) = n!/(n-k)!

